Melanie Butler reveals the trends hidden inside the inspection reports

The average quality of the language centres inspected by the British Council is continuing to go up. After deducting any needs for improvement, the mean average number of areas of strength awarded by inspectors, is now 5.5, up from 4.2 in 2017.

Does this mean that we’re looking at grade inflation? Statistically the answer is no. In fact, the distribution of scores awarded now looks much more like what you would normally expect than it was when we first analysed the figures in 2008. Back then, 40 per cent of schools scored zero points out of nine, and nobody at all got a perfect score. It looked less like a neat bell curve and more like a very steep descending staircase.

To make a statistical analysis, we are using the number of net areas of strength rather than the adjusted score used in the ranking, not least because it is the only way to calculate the change in scores over time. But also to discover the way scores are distributed, we need to use the raw data to calculate the standard deviation.

Help! Standard deviation, normal distribution, mean, average – isn’t this all getting a bit statistical? What next?

Bear with me. The statistics are really simple.

Mean and Median

Take a classic example of a normal distribution pattern: the height of American men. Their mean average height is 5 foot 10 (1.78 metres). Half the male population are that height or shorter, and half are that height or taller so that makes it the median average too.

Now let’s look at language centres. The mean average score of a UK language centre is 5.5 the median average is five. The mean is close to the median. So far, the distribution of scores looks pretty normal.

Standard Deviation

About 68 per cent of US males re within four inches (10 centimetres) of the average height. They are between 6 ft 2 (1.88 metres) and 5 ft 6 inches (1.67 metres) tall. Those four inches are the standard deviation.

The standard deviation for language schools is four net areas of strength. So, in a normal distribution curve most schools would score between four points above the mean and four points below. If we look at schools scoring between 1 area of strength and nine, we find 76 per cent do.

Seventy-six per cent is a little bit more than you would expect to see in a normal distribution. That is, partly, because not many centres are more than one standard deviation below the mean.

Fat Tail

However, 17 per cent of centres are extremely good. Statistically they are more than one standard deviation above the norm. That means they score more than 4 points above the average. Most score between five and eight points above the mean. They are equivalent to men who are 6 ft 3 (1.90m) to 6 ft 6 in tall.

Furthermore, two percent of centres are two standard deviations above the mean: they score nine or ten point above average. Statistically, these schools are giants.

Statisticians would say that the population of accredited schools in the UK has a long tail at the top. There are more high performing schools than you would expect.

One reason for this is that the most common score, the mode average, awarded by the British Council is three areas of strength. Normally statisticians would expect it to be more or less the same as both the mean average and the median, in this case 5 and 5.5.

And looking at these figures, they would expect the most common score would go up to meet the mean, gradually pushing the average up with it.

Indeed, this is exactly what has happened with the scores of accredited language schools since the Gazette first started publishing them in 2008.

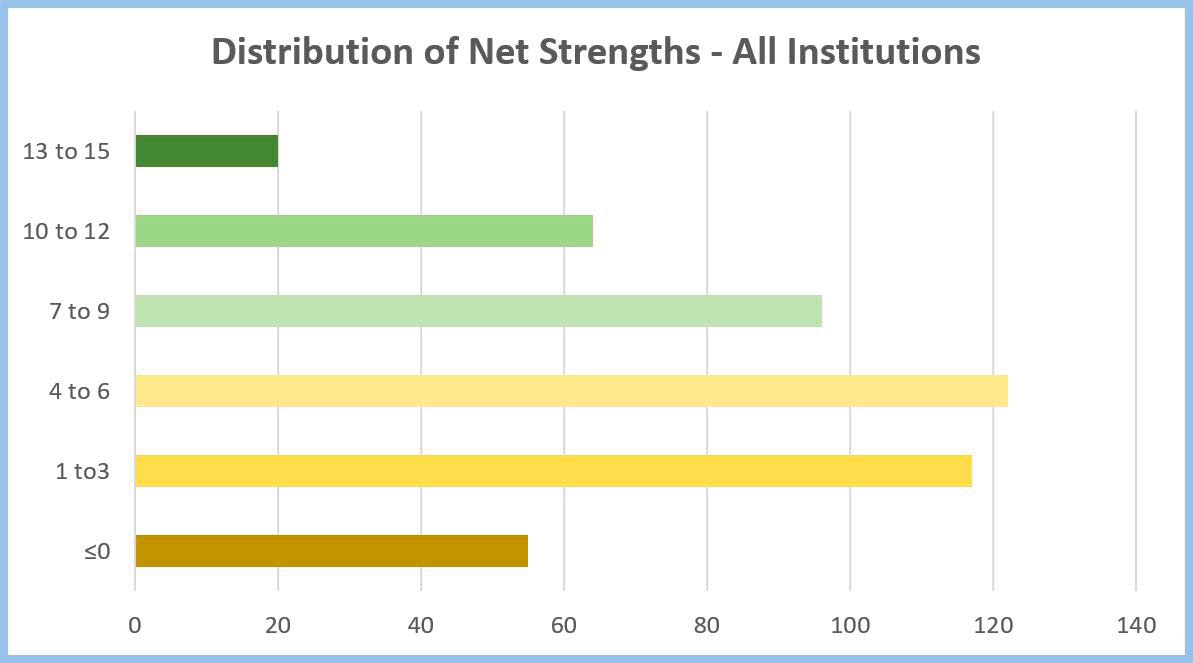
13 to 15        These centres are two SD above the mean, making them statistically outstanding

10 to 12        These centres are one SD above the mean, making them signifi cantly better than average.

7 to 9            These centres are within one SD from the mean.

4 to 6            Includes both the mean core and the median, or midpoint core and, as expected, represents the peak of the bell curve.

1 to 3            Includes the mode, or most common, score of 3.

0 or below     These centres are one Standard Deviation below the mean average score of 5 net strengths.